Calculating RMS in digital audio

[ccaudle (Chris)]

@abyss

I thought the range of amplitude was 1 to -1

I think just a little bit too rushed in the writing. The correct way to describe it is that the peak of a sine wave is 0 dB referenced to max digital value. That way if you have a peak meter or an RMS meter it will still show 0dB (assuming the RMS meter is calibrated correctly).

@abyss

Zero dBFS refers to (nearly?) maximum power not maximum amplitude

Dissipated power would depend on the load impedance, and so you would have to specify the impedance (like the dBm value specified 600 Ohm load).
The dB FS measurement is defined as an amplitude measurement, not power (as previously pointed out).

[lherg]

@abyss

@Robin, I’d like your opinion on this statement by lherg:

The advantage of this choice [max sized sine wave for dBFS] is that the peak of a 0 dB FS sine wave will also be 0.

A screenshot of Ardour and some x42 meters:

[x42 (Robin Gareus)]

@abyss

I thought the range of amplitude was 1 to -1. I would expect zero amplitude to be in the middle.

That part is correct. zero amplitude is silence, and hence -inf dB.

Max amplitude is either -1 or +1. A digital peak meter takes the abs() value, here RMS uses a square (the value is always positive. in both cases the range [0…1] is mapped from [-inf to 0] dB.

[abyss]

Robin, for the digital peak meter do you mean the range [0…1] is mapped in a linear way to the range [-inf…0]? If so, I don’t know why the ‘true-peak’ scale (thanks lherg) is not labeled with [0% to 100%]. If you mean mapped from amplitude/voltage to power/loudness in actual dBFS units, then how is that any different and differently useful to RMS on the dBFS scale? I am guessing the former linear mapping is what was meant. Wait, maybe you have instantaneous power in the digital peak meter and ‘smooooth’ power with RMS. There are three kinds of LUFS with regard to time interval of calculation. Maybe this is like that.

[lherg]

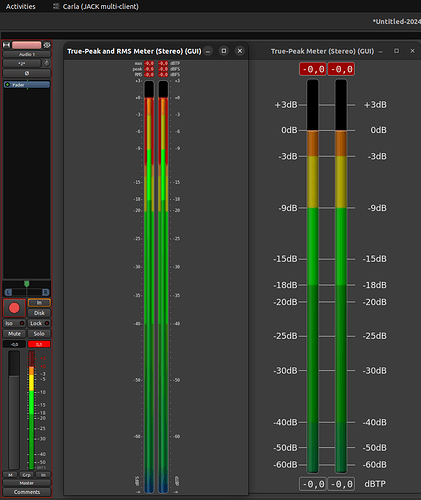
Why monitoring peak:
In the days of analog audio, equipment was much more tolerant of amplitude peaks.

If the maximal levels were exceeded, this would cause signal distortion, which is not necessarily unpleasant (if you like AC/DC or tube amps)

Additionally, many professional audio equipment had input tolerances well above the maximum level of broadcast standards, which also differed by country: https://en.wikipedia.org/wiki/Peak_programme_meter

Another example of this is magnetic tape, which in a way behaves like a compressor:
https://fr.wikipedia.org/wiki/Hyst%C3%A9r%C3%A9sis_magn%C3%A9tique#/media/Fichier:Power_Transformer_Over-Excitation.gif

With digital audio, exceeding the maximum level is catastrophic. This is why it is necessary to monitor peaks.

Why True peak:
In digital audio, the peak will give you the maximum value of the amplitude before analog conversion. But the problem is that when converting to analog, an analog signal will be created and potentially have higher peak values. Hence the need to calculate the True Peak even approximately.

Why LUFS
The sound level sensations perceived with your ears are different depending on the frequencies and acoustic power levels:
https://en.wikipedia.org/wiki/Loudness#/media/File:Lindos1.svg

This is why it is recommended to set a reference level for your monitoring speakers. And to have several monitoring speakers (a small system and a large one).

I don’t use LUFS but I understand it as a measurement system which does not calculate the average of the signal in the entire bandwidth but by decomposing the signal into different frequency bands, to calculate the average values ​​by bands, weights everything according to the ear response curve.

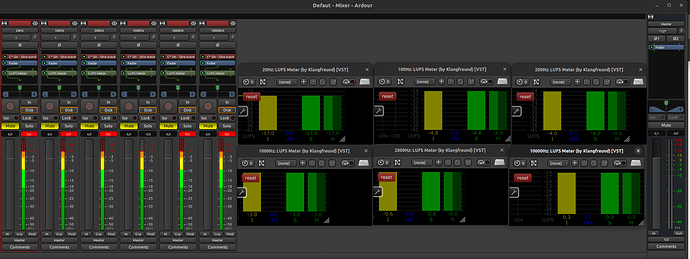
You can easily do this test with Ardour and a frequency generator.

You can see that the dbFS level of ardor is at 0dBFS for these signals (20Hz, 100Hz, 200Hz, 1000Hz, 2000Hz, 10000Hz), but that depending on the frequency the LUFS level is different. If you listen to the tracks one by one you can feel a different level sensation.

[abyss]

Nice explanation on the utility of true peak monitoring, lherg. Thanks.

[paul (Paul Davis)]

The problem with “true peak” is that computing it accurately requires knowing the internal architecture of the DAC, which is generally not available.

Consequently, typical best practices involve mixing so that peak values are just slightly below 0dBFS (and indeed, Ardour will show clip warnings just slighly below 0dBFS), to ensure that “inter-sample peaks” do not exceed 0dBFS.

[abyss]

Thanks for your insight, Paul.